Âge d'or de la cryptographie
Enjeux en cryptographie
Dans le code de César, le chiffre de Vigenère et Enigma, tout comme dans les systèmes cryptographiques contemporains, on retrouve les éléments suivants:
- Le message en clair: (en anglais, “cleartext”) ce qu’on veut chiffrer
- Le message chiffré: (en anglais, “ciphertext”) le résultat du chiffrement
- Le chiffre: (en anglais, “cipher”) la méthode utilisée pour chiffrer
- La clé: l’information secrète qu’on utilise pour chiffrer et déchiffrer les messages
Le but d’un système cryptographique est de rendre très difficile (idéalement, impossible) de dériver le message en clair à partir du message chiffré si on ne possède pas la clé. Pour bien des systèmes cryptographiques, il est moins difficile de se procurer la clé que de déchiffrer le message. Un problème se pose alors : celui de s’assurer que la clé demeure secrète.
Même si on utilise des chiffres de plus en plus complexes, qui prendraient en théorie 300 ans à déchiffrer avec les ordinateurs les plus puissants, le code ne sert plus à rien si la clé tombe entre les mains de ceux à qui elle n’est pas destinée. Ainsi pendant des centaines et des centaines d’années, de Jules César à la machine Enigma utilisée durant la seconde guerre mondiale, le problème de la confidentialité de la clé est demeuré central. Jusqu’à 1976, où deux mathématiciens ont eu une idée révolutionnaire.
Échange de clés Diffie-Hellman
Whitfield Diffie et Martin Hellman ont décrit en 1976 un mécanisme d’échange qui permet à deux interoculteurs d’utiliser la même clé sans jamais que celle-ci ne soit échangée entre les deux. Lorsque deux personnes veulent utiliser la même clé, ils peuvent s’échanger seulement une partie de l’information et utiliser cette information pour calculer la valeur de la clé. Le principe est le suivant:
- A et B s’entendent sur une information commune (un nombre), x
- A définit une valeur secrète, y, « mélange » x et y et transmet le résultat xy à B
- B définit une valeur secrète, z, « mélange » x et z et transmet le résultat xz à A
- A mélange xz et y et obtient la clé xyz
- B mélange xy et z et obtient la clé xyz
La force de ce système est qu’il est pratiquement impossible d’extraire x ou y du “mélange” xy, et que ni x ni y n’ont été échangés.
L’algorithme Diffie-Hellman est le suivant:
- A et B échangent 2 nombres : un nombre premier P et un générateur G
- A et B choisissent des nombres secrets X au hasard. Ces nombres doivent être inférieurs à P.
- A et B calculent chacun Y à partir de leur propre X et des deux valeurs initiales, selon la formule
Y = G^X % P, et transmettent le résultat à l’autre - A et B calculent la clé C à partir du Y de l’autre et de leur propre secret :
C = Y^X % P
La clé calculée ainsi par A et B ne sera utilisée que pour cette communication: c’est pour cette raison qu’on l’appelle clé de session.
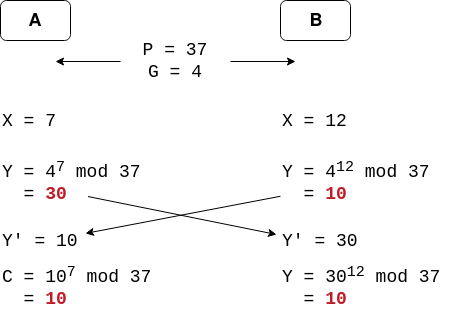
Le schéma suivant donne un exemple de son fonctionnement:
Dans cet exemple, A et B s’entendent sur des valeurs pour P et G (respectivement 37 et 4). Pour la valeur de X, A choisit 7 et B choisit 12. La clé calculée par A et B à partir de ces valeurs vaut 10.
Cette manière de s’échanger une clé de chiffrement est utilisé dans plusieurs protocoles de communication, notamment HTTPS.
Pour calculer une clé temporaire selon la méthode Diffie-Hellman, A et B s’entendent sur les valeurs suivantes: P=57 et G=14. A choisit X=5 et B choisit X=16. Quelle est la valeur de la clé finale? Vous pouvez utiliser la calculatrice sur le site https://planetcalc.com/8326/.
Y = G^X % PC = Y^X % P
Clés publiques
Les travaux de Diffie et Hellman ont pavé la voie à une deuxième manière de régler le problème de l’échange de clé. La cryptographie à clé publique a été mise au point en 1978 par trois cryptologues: Ronald Rivest, Adi Shamir et Leonard Adleman. L’algorithme se nomme RSA, des noms de ses trois inventeurs.
Dans leur système, on utilise deux clés différentes : une pour chiffrer le message, et une autre pour le déchiffrer. Comme le fait de chiffrer un message ne pose pas de problème de confidentialité particulier, la clé de chiffrement peut être diffusée à n’importe qui: c’est la clé publique. La clé qui sert à déchiffrer le message, elle, doit cependant demeurer secrète: c’est la clé privée. Les deux clés fonctionnent exclusivement l’une avec l’autre, comme un cadenas et sa combinaison.
Imaginons deux personnes (Alice et Bob) qui veulent s’envoyer des colis par la poste en s’assurant que personne ne puisse en voir le contenu. Comment pourraient-elles procéder? Une solution possible serait que chacune achète une clé et un cadenas. Ensuite, Alice donne son cadenas à Bob et Bob donne le sien à Alice, mais chacune conserve précieusement sa clé. Lorsque Bob voudra envoyer un colis à Alice, il lui suffira de le mettre dans une boîte puis de fermer la boîte avec le cadenas d’Alice. Puisque seule Alice possède la clé pour ouvrir le cadenas, le contenu du paquet restera confidentiel durant son trajet. Un système de chiffrement par clé publique fonctionne de la même manière. La clé publique est le cadenas, on peut en faire un nombre illimité de copies et les distribuer à n’importe qui; on s’en sert pour chiffrer les données. La clé privée cependant doit rester secrète et être protégée, car c’est elle qui est utilisée pour déchiffrer les messages.
Le terme chiffrement symétrique désigne un système de chiffrement qui utilise la même clé pour chiffrer et déchiffrer les messages. Les termes chiffrement asymétrique ou chiffrement par clé publique désignent un système de chiffrement qui utilise des clés différentes pour chiffrer et déchiffrer les messages. Visonnez la vidéo Chiffrement symétrique ou asymétrique, quelle différence ? pour une vulgarisation des différences entre les clés symétriques et asymétriques.
La cryptographie par clé publique est très utile et a de nombreuses applications (chiffrement, signatures numériques, authentification, certificats…), mais elle est beaucoup plus coûteuse en termes de ressources que la cryptographie symétrique. C’est pourquoi les deux types de chiffrement sont utilisés aujourd’hui de manière complémentaire.
Applications
Échange de clés
Un des usages de l’algorithme RSA est de chiffrer une clé symétrique afin de pouvoir la transmettre de manière sécuritaire entre deux interlocuteurs. RSA est donc dans ce contexte une alternative à l’échange de clés Diffie-Hellman. Le principe est le suivant:
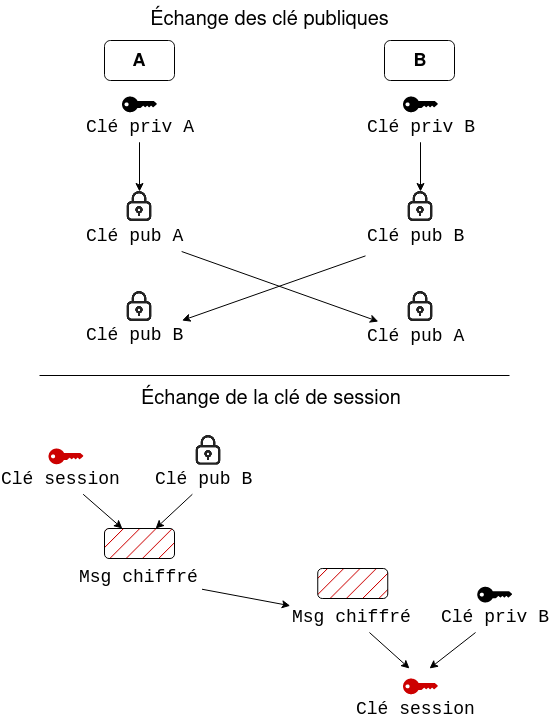
A et B s’échangent d’abord leurs clés publiques respectives. Ceci n’a lieu qu’une seule fois.
Ensuite, chaque fois que A et B veulent communiquer ensemble, une des deux participants (ici, A) doit créer une clé pour l’occasion (la clé de session).
A utilise la clé publique de B pour chiffrer cette clé afin de la transmettre à B de manière confidentielle. B utilise ensuite sa clé privée pour déchiffrer le message de A, qui contient la clé de session. Dès lors A et B ont la même clé de session et peuvent communiquer de manière confidentielle.
Authentification
Le chiffrement par clé publique peut aussi être utilisé à des fins d’authentification.
On utilise généralement les mots de passe pour s’authentifier sur de nombreux sites. Le mot de passe est une façon de prouver que nous somme bien la personne qu’on prétend être, car un mot de passe, normalement, est secret et connu uniquement de nous. Mais les mots de passe peuvent parfois faire l’objet d’attaques, et ne sont pas une mesure de sécurité très fiable lorsque les utilisateurs choisissent des mots de passe faciles à deviner.
Une méthode plus sécuritaire et pratique consiste à utiliser une clé privée. Comme un mot de passe, une clé privée est un secret que seul l’utilisateur devrait posséder et ne divulguer à personne. Une clé privée est cependant beaucoup plus sécuritaire qu’un mot de passe car elle est:
- Générée aléatoirement
- D’une taille largement supérieure aux mots de passe les plus complexes
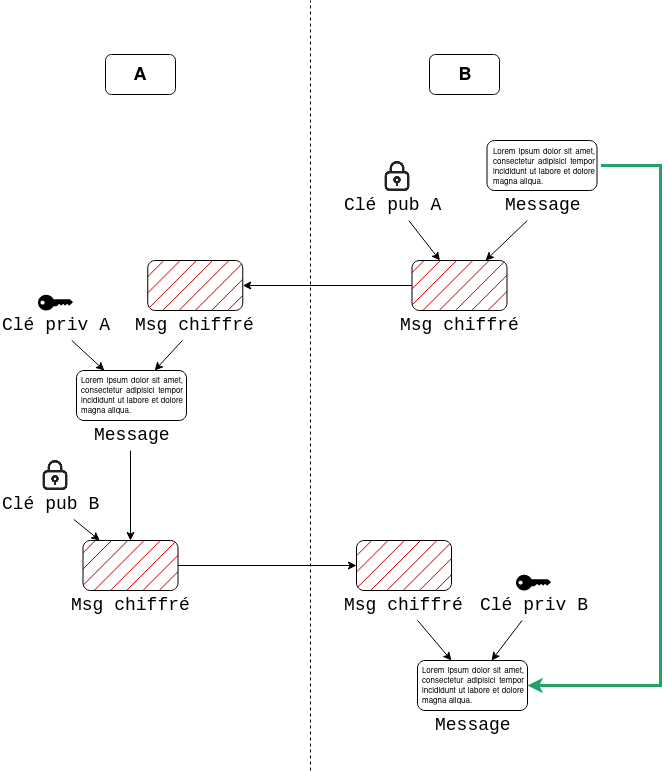
Les clés privées sont donc beaucoup moins vulnérables aux attaques par force brutale que les mots de passe. Comment peut-on alors utiliser la cryptographie asymétrique pour l’authentification? Le principe est très simple: si je chiffre un message avec la clé publique d’Alice et qu’elle arrive à le déchiffrer, elle me prouve qu’elle possède la clé privée correspondante, et je peux donc présumer qu’elle est bien Alice. Le schéma suivant illustre le fonctionnement (on suppose que l’échange de clés publiques a déjà eu lieu):
Dans cet exemple, A veut s’authentifier à B.
- B génère un message qu’il chiffre avec la clé publique de A
- A reçoit le message et le déchiffre avec sa clé privée
- A chiffre à son tour le message avec la clé publique de B
- B reçoit le message et le déchiffre avec sa clé privée
- Si le résultat est le même message que celui d’origine, A a prouvé son identité à B
OpenSSL
OpenSSL est un logiciel libre (sous licence Apache) qui fournit une suite très complète de programmes pour effectuer les opérations cryptographiques courantes: chiffrer et déchiffrer des messages, générer des clés symétriques ou des paires de clés publique et privée, et de nombreuses autres fonctionnalités. On peut utiliser OpenSSL comme une librairie dans plusieurs langages et il est accessible à partir de la ligne de commande dans la plupart des distributions linux. OpenSSL est largement utilisé par les navigateurs web, les serveurs web, les clients et serveurs de messagerie, les VPN (Virtual Private Networks), et d’autres applications qui utilisent la cryptographie.
À partir de la ligne de commande linux, la liste des commandes, des fonctions de hachage et des chiffres disponibles peut être affichée comme suit:
openssl helpChiffrement symétrique avec DES
Le Data Encryption Standard est un algorithme de chiffrement symétrique développé dans les années 1970 et qui a été utilisé plusieurs années, jusqu’à ce que des chercheurs démontrent en 1999 une méthode pour le briser. Malgré qu’on recommande de ne pas l’utiliser dans des contextes où la confidentialité est importante, il est tout de même implémenté dans OpenSSL.
Générer une clé
Pour encoder et décoder avec l’algorithme DES, il nous faut tout d’abord créer une clé symétrique (un nombre aléatoire de 128 bits fera l’affaire). On la génère comme suit:
openssl rand 128 > cle.binQu’est-ce qui s’affiche à l’écran si on ne met pas > cle.bin à la fin de la commande? À quoi sert cette partie de la commande?
Chiffrer et déchiffrer un message
La syntaxe de la commande enc, qui sert à chiffrer/déchiffrer avec DES, est la suivante:
openssl enc -in FICHIER (-out FICHIER) {-e|-d} -CHIFFRE -k CLE (-a)
# Pour chiffrer un fichier avec la cle 'cle.bin'
openssl enc -in msgClair.txt -out msgChiffre.bin -e -des3 -k cle.bin
# Pour déchiffrer un fichier avec la cle 'cle.bin'
openssl enc -in msgChiffre.bin -out msgDechiffre.txt -d -des3 -k cle.bin| Option | Signification |
|---|---|
| -in | Nom du fichier en entrée. |
| -out | Nom du fichier où écrire le résultat de l’opération. Si absent, le résultat est affiché à l’écran. |
| -e | Signifie qu’on veut chiffrer (“encrypt”) le fichier en entrée. |
| -d | Signifie qu’on veut déchiffrer (“decrypt”) le fichier en entrée. |
| -CHIFFRE | Remplacer “CHIFFRE” par l’algorithme de chiffrement (les choix possibles sont affichés avec openssl help) |
| -k | Le fichier qui contient la clé. |
| -a | Cette option (facultative) indique que le message chiffré est encodé en base64, un format qui permet de représenter des données binaires de manière assez compacte en utilisant un jeu de 64 caractères. |
Le fichier message1.bin contient un message chiffré à l’aide de l’algorithme DES-EDE3 avec cette clé. Utilisez la même clé pour le déchiffrer. Quel est le message en clair?
Chiffrement symétrique avec AES
Le Advanced Encryption Standard est un algorithme de chiffrement symétrique développé au début des années 2000 suite à la découverte des lacunes du DES. Il est encore aujourd’hui considéré comme très robuste et est utilisé dans un grand nombre d’applications où la confidentialité est centrale.
La commande OpenSSL pour chiffrer/déchiffrer des messages avec AES utilise un mot de passe plutôt qu’un clé numérique. La syntaxe est la suivante:
openssl CHIFFRE -in FICHIER -out FICHIER -pass:FICHIER{-e|-d} (-a)
# Pour chiffrer un fichier avec AES-256 et la clé 'clé.bin'
openssl aes-256-cbc -in msgClair.txt -out msgChiffre.bin -pass file:cle.bin -e
# Pour déchiffrer un fichier avec la clé 'clé.bin''
openssl aes-256-cbc -in msgChiffre.bin -out msgDechiffre.txt -pass file:cle.bin -d L’option -pass file: donne le nom du fichier qui contient la clé. Si elle n’est pas spécifiée, la clé doit être saisie par l’utilisateur.
- Le fichier message2.bin contient un message chiffré à l’aide de l’algorithme AES-256-ECB et la clé
edrv#90%!. Décodez-le; quel est le message en clair?
- Voici quelques indices:
- Faites un
wget https://otardi.gitlab.io/420-313/exercices/message2.bindepuis la VM pour télécharger le fichier. - Puis “touch cle.bin”
- “nano cle.bin” (inserer
edrv#90%!dans lecle.bin). - Enfin, exécutez
openssl aes-256-ecb -in message2.bin -out message2Clear.txt -pass file:cle.bin -d
- Faites un
- À l’aide de l’algorithme AES-256-ECB et d’une clé de votre choix, chiffrez les trois fichiers suivants: fichier1.txt (8 octets), fichier2.txt (87 octets), fichier3.txt (583 octets). Quelles sont les tailles des fichiers chiffrés résultants?
Chiffrement par clé publique avec RSA
Dans OpenSSL, 3 commandes servent à effectuer les opérations requises par l’algorithme RSA:
genrsa- Pour créer une clé privéersa- Opérations sur les clé: dérivations, conversions, etc.pkeyutl- Opérations utilisant les clés: chiffrement, déchiffrement, etc.
Créer une clé privée
Lors de la création de la clé il faut spécifier une taille entre 512 et 16384 bits. Plus cette taille est grande, plus le chiffrement sera sécuritaire; mais en contrepartie les opérations de chiffrement et de déchiffrement prendront plus de temps. Au fil des années, avec l’augmentation des capacités de calcul des processeurs, la taille qu’on considérait sécuritaire pour une clé RSA a augmenté. Aujourd’hui on estime que 2048 bits est une taille suffisante pour résister aux attaques.
Contrairement aux algorithmes symétriques, les clés RSA sont encodées en base64.
La syntaxe de la commande est la suivante:
openssl genrsa -out FICHIER TAILLE
openssl genrsa -out cle.privee 2048Créer une clé publique
Nous avons vu qu’avec la cryptographie par clé publique, les clés viennent par paires: un message chiffré avec une clé publique donnée ne peut être déchiffrée qu’avec la clé privée correspondante. Cette dépendance entre les deux clés vient du fait que la clé publique doit être dérivée de la clé privée (c’est-à-dire qu’on la génère à l’aide de fonctions mathématiques appliquées sur la clé privée). Note importante, cette dérivation est à sens unique: il est impossible de dériver, à l’inverse, une clé privée à partir de la clé publique.
La syntaxe de la commande pour créer une clé publique est celle-ci:
openssl rsa -pubout -in FICHIER -out FICHIER
openssl rsa -pubout -in cle.privee -out cle.publiqueL’option -pubout signifie qu’on veut que le fichier de sortie soit la clé publique.
Chiffrer un message
Pour chiffrer un message, on doit spécifier les fichiers d’entrée et de sortie, le fichier de la clé et le fait que celle-ci soit la clé publique:
openssl pkeyutl -encrypt -inkey FICHIER -pubin -in FICHIER -out FICHIER
openssl pkeyutl -encrypt -inkey cle.publique -pubin -in message.txt -out message.bin| Option | Signification |
|---|---|
| -in | Nom du fichier en entrée. |
| -out | Nom du fichier où écrire le résultat de l’opération. Si absent, le résultat est affiché à l’écran. |
| -encrypt | Signifie qu’on veut chiffrer le fichier en entrée. |
| -inkey | Nom du fichier qui contient la clé utilisée pour chiffrer le message. |
| -pubin | Spécifie que la clé utilisée pour chiffrer le message est la clé publique. |
Déchiffrer un message
La commande est la suivante:
openssl pkeyutl -decrypt -inkey FICHIER -in FICHIER -out FICHIER
openssl pkeyutl -decrypt -inkey cle.privee -in message.bin -out dechif.txt- Le fichier privee.rsa contient une clé privée. Utilisez-la pour déchiffrer ce message. Que contient-il?
- À partir de cette clé privée, générez une clé publique et utilisez-la pour chiffrer fichier4.txt (187 octets). Quelle est la taille en octets du message chiffré?
- Quelqu’un vous envoit une clé de session chiffrée avec votre clé publique et un message chiffré (AES-256-CDC) avec cette clé de session. Que contient le message? Référez-vous à la section sur l’échange de clé de session avec RSA
À consulter
- Échange de clés Diffie-Hellman (Khan Academy, anglais)
- Chiffrement à clé publique
- Comprendre les chiffrements